算数の解説が続いたので、数学の解説を…
気が付けば、この地域は「中間テスト２週間前」に入りました！
中学３年生最初の定期テスト(数学)は、多くの学校が「展開因数・分解」がメインになると思います。
今回は、その中でもつまづく人が多い(＝差が付きやすい)
S＝aℓ の証明を扱います！
…が、せっかくのブログで説明するだけでは全く面白くない！！
今日は外は雨。少し時間もあるので、「この問題を使って遊んでみよう♪」と思います！
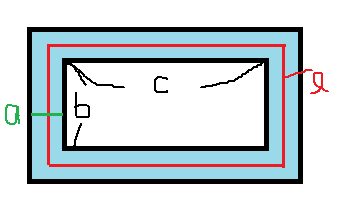
【問題】※手書きでスイマセン
図のような長方形の土地の外側に、幅a(緑線)の道(薄青)がある。この道の面積をS
道の中央を通る線(赤線)の長さをℓとするとき、S＝aℓ となる。
このことを、長方形の土地の縦の長さをb、横の長さをcとして証明せよ
手書きの図で申し訳ないm(__)m
これは、教科書にも必ずあるタイプの問題ですね！
今回は、「この問題で遊ぶ」のが目的なので、解答は簡略バージョンで！
【解答】
S＝(2a+b)(2a+c)-bc
=4a^2+2ab+2ac…①
ℓ＝2(a+b)+2(a+c)
＝4a+2b+2c…②
②より、aℓ＝a(4a+2b+2c)
＝4a^2+2ab+2ac…③
①＝③より、S=aℓ
とこんな感じです。
簡単に説明しておくと、、、
「道の面積Sは、大きな長方形から小さな長方形を引けば出るよ！」…①
「中央を通る線ℓは、縦の辺(a+b)と横の辺(a+c)がそれぞれ２本ずつあるから２倍して足すよ！」…②
「②で求めたℓにaをかければaℓが求められるよ！」…③
「あーら不思議！①＝③だね！つまり、S=aℓだね」
といった流れです。
では、遊んでみましょう♪
今回は折角なので、これを、「文字」ではなく「図形」としてなぜ成り立つのか？いったいどういうことなのか？を説明してみます^^
まずは、先程、証明で使用した図をバラバラに切りました！
４つの紙テープのような形になりました！
次に、この４つの紙テープを横一列に並べました！
少し曲がっていますがそこはご愛嬌で^^
こうすると、１つの平行四辺形と見立てることが出来ます！
(本当はもう少し切り分けて、長方形にした方が分かりやすいのですが)
平行四辺形の面積(S)＝底辺(赤線の長さ)×高さ(緑線の長さ)
となることが、目で見て分かるでしょうか？
つまり、S＝aℓの証明とは、「曲がった道を真っすぐにしたときの面積」
と考えることが出来ます！
実は、この考え方が分かると、図形の問題にも利用することができます！
長くなりましたので、続きは次回に！！